gp2Scale

gp2Scale is a special setting in fvgp that combines non-stationary, compactly-supported kernels, HPC distributed computing, and sparse linear algebra to allow scale-up of exact GPs to millions of data points. gp2Scale holds the world record in this category! Here we run a moderately-sized GP, just because we assume you might run this locally.

I hope it is clear how cool it is what is happening here. If you have a dask client that points to a remote cluster with 500 GPUs, you will distribute the covariance matrix computation across those. The full matrix is sparse and will be fast to work with in downstream operations. The algorithm only makes use of naturally-occuring sparsity, so the result is exact in contrast to Vecchia or inducing-point methods.

##first install the newest version of fvgp
#!pip install fvgp==4.2.0

Setup

import numpy as np
import matplotlib.pyplot as plt
from fvgp import GP
from dask.distributed import Client
%load_ext autoreload
%autoreload 2

client = Client() ##this is the client you can make locally like this or 
#your HPC team can provide a script to get it. We included an example to get gp2Scale going
#on Perlmutter


#It's good practice to make sure to wait for all the workers to be ready
client.wait_for_workers(4)

Preparing the data and some other inputs

def f1(x):
    return ((np.sin(5. * x) + np.cos(10. * x) + (2.* (x-0.4)**2) * np.cos(100. * x)))

input_dim = 1
N = 10000
x_data = np.random.rand(N,input_dim)
y_data = f1(x_data).reshape(len(x_data))
hps_n = 2

hps_bounds = np.array([[0.1,10.],      ##signal var of Wendland kernel
                       [0.001,0.02]])  ##length scale for Wendland kernel
        

init_hps = np.random.uniform(size = len(hps_bounds), low = hps_bounds[:,0], high = hps_bounds[:,1])

my_gp2S = GP(x_data,y_data,init_hps,  #compute_device = 'gpu', #you can use gpus here
            gp2Scale = True, gp2Scale_batch_size= 1000, gp2Scale_dask_client = client, info = True
            )

my_gp2S.train(hyperparameter_bounds = hps_bounds, max_iter = 2)

/home/marcus/Coding/fvGP/fvgp/gp.py:261: UserWarning: hyperparameter_bounds not provided. They will have to be provided in the training call.
  warnings.warn("hyperparameter_bounds not provided. "

KV sparsity =  0.03029374
CG solve in progress ...
CG compute time: 1.1873481273651123 seconds, exit status  0 (0:=successful)
Random logdet() in progress ...  1.1878197193145752 seconds.
Random logdet() compute time:  69.58024549484253 seconds.
KV sparsity =  0.03029374
CG solve in progress ...
CG compute time: 1.1581900119781494 seconds, exit status  0 (0:=successful)
Random logdet() in progress ...  1.1586105823516846 seconds.
Random logdet() compute time:  68.79514074325562 seconds.
KV sparsity =  0.02742228
CG solve in progress ...
CG compute time: 1.0823793411254883 seconds, exit status  0 (0:=successful)
Random logdet() in progress ...  1.0828258991241455 seconds.
Random logdet() compute time:  65.2050678730011 seconds.
KV sparsity =  0.02742228
CG solve in progress ...
CG compute time: 1.0921993255615234 seconds, exit status  0 (0:=successful)
Random logdet() in progress ...  1.0926308631896973 seconds.
Random logdet() compute time:  62.44978094100952 seconds.

x_pred = np.linspace(0,1,100) ##for big GPs, this is usually not a good idea, but in 1d, we can still do it
                              ##It's better to do predicitons only for a handful of points.

mean1 = my_gp2S.posterior_mean(x_pred.reshape(-1,1))["f(x)"]
var1 =  my_gp2S.posterior_covariance(x_pred.reshape(-1,1), variance_only=False)["v(x)"]

print(my_gp2S.get_hyperparameters())

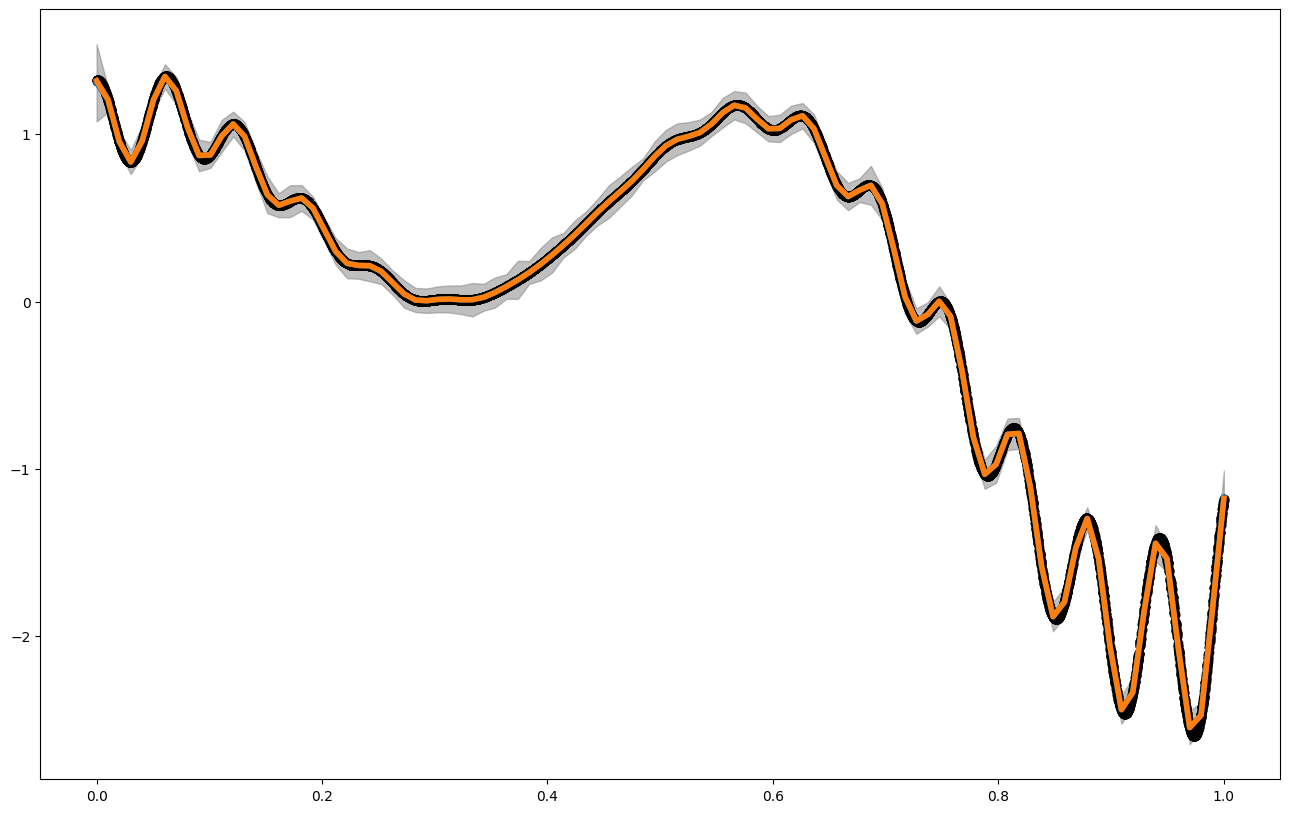
plt.figure(figsize = (16,10))
plt.plot(x_pred,mean1, label = "posterior mean", linewidth = 4)
plt.plot(x_pred,f1(x_pred), label = "latent function", linewidth = 4)
plt.fill_between(x_pred, mean1 - 3. * np.sqrt(var1), mean1 + 3. * np.sqrt(var1), alpha = 0.5, color = "grey", label = "var")
plt.scatter(x_data,y_data, color = 'black')

[2.55431933 0.01375789]

<matplotlib.collections.PathCollection at 0x7feba86da9e0>